【 問題 】4~5年生向け
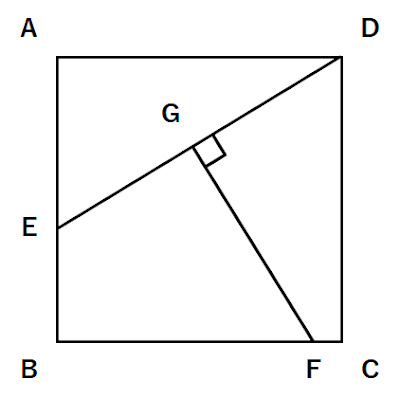
四角形ABCDは正方形で、点Eと点Fは正方形ABCDの辺上にあります。点GはDE上にあり、∠DGF=90°、GF=10㎝です。
また、三角形AEDと四角形GFCDと四角形EBFGの面積比は3:3:4です。
正方形ABCDの面積は何㎠ですか。
【 解答 】
パズルのThe-Tみたいだね。相似の基本が詰まった問題、相似比⇒面積比⇒相似比の順に出していくんだ。では、いきましょう。
AE:EBがすぐ出せる。
三角形AEDの面積:台形EBCDの面積
= 3:(4+3)
= 3:7
= AE:EB+DC
AE:EB+DC=3:7
⇒ AE:DC=3:(3+7)× 1/2
⇒ AE:DC=3:5
⇒ AE:EB:DC=3:2:5
AE:EB=3:2がすぐにわかった。
ここに絡めて直角三角形の相似を作るんだけど、この問題には以下の3パターンの直角三角形の相似が入ってる。
直角三角形の相似を頭に叩き込んでおこう。
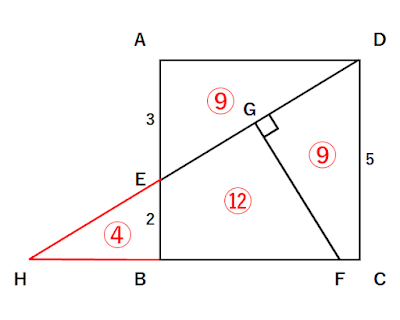
直角三角形の相似を目指して補助線を引くと次のような感じになる。
AE:EB=3:2
⇒ △EADの面積:△EBHの面積=9:4
⇒ △EADの面積=⑨、△EBHの面積=④
△EADの面積=⑨
△EAD:四角形GFCD:四角形EBFG=3:3:4
⇒ △EADの面積=四角形GFCDの面積=⑨、四角形EBFGの面積=⑫
できました☆
△EBHの面積=④、四角形EBFGの面積=⑫
⇒ △EBHの面積=④、△FGHの面積=⑯
⇒ △EBHの面積:△FGHの面積=1:4
⇒ EB:FG=1:2
⇒ FG=10㎝、EB=5㎝
EB:DC=2:5
EB=5㎝
⇒ DC=5㎝× 5/2=25/2㎝
正方形ABCDの面積
= 25/2㎝ × 25/2㎝ = 625/4㎠
△EAD∽△EBH∽△FGH∽△DCH
この4つの三角形が相似だ。
相似比は3:2:4:5だよ、確認してね!
よって、答えは625/4㎠となる。
にほんブログ村