倍数算１４。

 【 問題 】３～４年生向け

Aさんの所持金はBさんの所持金の3倍でした。文房具屋さんで使った金額が、AさんはBさんの5倍だったので、2人の残金はともに400円になりました。Aさんのはじめの所持金はいくらでしたか。

【 解答 】

勉強は反復が大事。納得がいくまで繰り返そう。

では、まいります。

差が一定の倍数算だね。

（ Read more » cf.倍数算1 ）

Aさんのはじめの所持金＝③

Bさんのはじめの所持金＝①

⇒ AさんはBさんより③－①＝②だけ多く持ってた

Aさんの使った金額＝ 5 

Bさんの使った金額＝ 1 

⇒ AさんはBさんより 5 － 1 ＝ 4 だけ多く使った

この②と 4 が等しいんだ。

だって、残金が同じになったんでしょ？ということは、Ａさんは、多く持ってた分だけ多く使ったんだ。

②＝ 4 

⇒ ①＝ 2 、③＝ 6

できました☆

Aさん＝③－ 5 ＝ 6 － 5 ＝400円

Bさん＝①－ 1 ＝ 2 － 1 ＝400円

⇒ 1 ＝400、 2 ＝800、5 ＝2000、 6 ＝2400

まとめると

Aさん＝2400円－2000円＝400円

Bさん＝800円－400円＝400円

はじめの所持金は3倍、使った金額は5倍、残金はともに400円になってるね！くどくどと確認しよう！

よって、答えは2400円となる。

にほんブログ村

中学校受験ランキング

数の性質１５。

 【 問題 】５年生向け

4けたの整数である8AB1を2けたの整数であるABで割ったところ、商が整数で割り切れました。2けたの整数ABはいくつですか。ただし、2けたの整数ABは50より小さい整数とします。

【 解答 】

中学受験では早めの準備・対策が有効で、5年生くらいまでには算数なり理科なり、どの科目でもいいんだけど、気持ち的に追われない科目が1つあると良いと思う。

では、いきましょう。

8AB1÷AB＝整数

⇒ 8AB1はABの倍数

これはいいね。

ここで8AB1からAB0を引き算してあげる。

どういうことかというと

AB0＝AB×10

だから、当然、AB0はABの倍数だよね。

8AB1はABの倍数で、AB0もABの倍数、ということは

8AB1－AB0＝8001＝ABの倍数

になる。

ABの倍数からABの倍数を引いたら、その答えは当然、ABの倍数になるね。

そう、8001はABの倍数なんだ。

8001はどういう数字か調べてみると、9で割れるとわかるから、9で割ってみる。

8001＝9×889

889は7で割れるね。

8001＝9×7×127

9は3×3だから、もう少し細かくしてみる。

8001＝3×3×7×127

これ以上は細かくならないね（127は素数だね）。

8001＝3×3×7×127、これをよく見ながら考える。

8001は、3の倍数でもあるし、7の倍数でもあるし、3×3＝9の倍数でもあるし、3×7＝21の倍数でもあるし、3×3×7＝63の倍数でもあるし、127の倍数でもあるし、、、

8001はABの倍数で、ABは50未満とあるから、AB＝21で確定する。

AB＝21を入れて確認すると

8211÷21＝391

となって、ちゃんと割り切れるね。

よって、答えは21となる。

にほんブログ村

中学校受験ランキング

倍数算１３。

 【 問題 】３～４年生向け

貯金箱に5円玉のみ169枚が入ってます。11月13日から毎日、貯金箱に5円玉1枚、10円玉3枚を入れていきます。

（１）5円玉と10円玉の枚数の比が16：9になるのは何月何日ですか。

（２）(１) のとき、貯金箱に入ってる5円玉と10円玉の合計金額は何円ですか。

【 解答 】

受験生は1週間があっという間に感じるはず。1日1日を大切に過ごそう。

では、まいります。

（１）

5円玉と10円玉の枚数の比が16：9になる、とあるけど、10円玉は元々0枚なんだから、この16：9の9の枚数は、入れた枚数に等しい。

（ Read more » cf.倍数算11 ）

5円玉＝⑯枚、10円玉＝⑨枚になったと考えると、入れた10円玉の枚数はもちろん⑨枚。入れた10円玉の枚数が⑨枚なら、入れた5円玉の枚数は⑨×1/3＝③枚となる。

5円玉  ：169枚＋③＝⑯

10円玉：　0枚＋⑨＝⑨

上の式をよく見てよく考えて欲しい。

よく理解できたらあとは解くだけ。

169＋③＝⑯

⇒ ⑬＝169

⇒ ①＝13

⇒ ③＝39、⑨＝117、⑯＝208

5円玉  ：169枚＋39枚＝208枚

10円玉：  0枚＋117枚＝117枚

5円玉を39枚、10円玉を117枚入れると、枚数の比は208：117＝16：9になったんだ。

5円玉は1日1枚、10円玉は1日3枚入れるんだから

39÷1＝117÷3＝39日

39日かかる。

39日かかるってことは、11月13日から数えて39日目を出せばいい。

11/13から数えて39日目

＝ 11/13の38日後

＝ 11/51

＝ 12/21

（ Read more » cf.日暦算1 ）

よって、答えは12月21日となる。

（２）

（１）でもう出したね。

5円玉は208枚、10円玉は117枚

⇒ 5×208＋10×117＝2210円

よって、答えは2210円となる。

にほんブログ村

中学校受験ランキング

場合の数２０。

 【 問題 】３～４年生向け

2001～2026の26個の数字から2個の数字を選んでかけ算して、その答えを10で割ったところ余りが9になりました。このような2個の数字の選び方は何通りありますか。ただし、2001と2026、2026と2001、は同じ選び方とします。

【 解答 】

やることが多くて大変だけど、一貫性だけは必ず意識して、手応えのある勉強を積み重ねていこう。

では、いきましょう。

10で割ると余りが9

＝ 1の位が9

これはいいね。

2個の数字をかけ算すると1の位が9になったんだ。

たとえば、どんなのがあるか。

2001×2009＝4020009

とか

2003×2013＝4032039

とか

2007×2017＝4048119

とか

・・・

そう、2個の数字の1の位が（1、9）（3、3）（7、7）だったら、かけ算すると1の位が9になるんだ。1の位だけに着目すればいいんだね。

1の位が1の数字

＝ 2001、2011、2021の3個 ・・・ Aグループ

1の位が3の数字

＝ 2003、2013、2023の3個 ・・・ Bグループ

1の位が7の数字

＝ 2007、2017の2個 ・・・ Cグループ

1の位が9の数字

＝ 2009、2019の2個 ・・・ Dグループ

（1、9）は、Aから1個とDから1個を選ぶ

⇒ 3×2＝6通り

（3、3）は、Bから2個を選ぶ

⇒ 3通り

（7、7）は、Cから2個を選ぶ

⇒ 1通り

これらを足してあげれば答えだ。

6＋3＋1＝10通り

1の位に着目するんだから、2001～2026でも、1～26でも、答えは同じ10通りになる。地道に順々に数えてもいけそうでしょ？数が大きくても臆したり焦ったりしちゃダメだよ！

よって、答えは10通りとなる。

にほんブログ村

中学校受験ランキング

場合の数１９。

 【 問題 】１～４年生向け

０、０、０、４、６、７の6個の数字があります。この6個の数字を並びかえて6桁の整数を作ります。

（１）一番大きい整数と一番小さい整数の差はいくつですか。

（２）全部で何通りの整数ができますか。

【 解答 】

ミス込みで実力なんて言ってたらダメだ。普段から丁寧を心掛ける。ノーミスを決めて上を追うんだ！

では、いきましょう。

（１）

一番大きい整数＝764000

一番小さい整数＝400067

⇒ 764000－400067＝363933

よって、答えは363933となる。

（２）

10万の位に0は使えないから、10万の位は4か6か7のどれか。

10万の位が7のときを考えてみる。

７▢▢▢▢▢

▢には0、0、0、4、6が入るんだけど、何通りだろう。

0は3個あるから後回しにして、4と6から入れてみる。

７▢▢▢▢▢

▢は5カ所あるから、4の置き場所は5通りある。

７▢４▢▢▢

例えば、上のように2番目の▢に4を入れたとすると残りの▢は4ヶ所だから、6の置き場所は4通りある。

７▢４▢▢６

6を最後の▢に入れたとすると上のようになって、残りの3カ所の▢には自動的に0が入る。

７０４００６

もうわかったね。

７▢▢▢▢▢

▢には0、0、0、4、6が入るんだけど、まず4の置き場所は5カ所あるから5通り、続いて6の置き場所は4ヶ所あるから4通り、残りの3カ所には自動的に0が置かれる。

⇒ 5×4＝20通り

そうなんだ、4と6の置き場所を決めてしまえばいいんだ。

0、0、0、4、6の並びかえ

⇒  5×4＝20通り

てことだね。

〈類題〉

AAABCの並びかえは何通り？

⇒ 5×4＝20通り（BとCの置き場所を決める）

☆☆▢△の並びかえは何通り？

⇒ 4×3＝12通り（▢と△の置き場所を決める）

12333の並びかえは何通り？

⇒ 5×4＝20通り（1と2の置き場所を決める）

7899の並べかえは何通り？

⇒ 4×3＝12通り（7と8の置き場所を決める）

XXXXYZの並べかえは何通り？

⇒ 6×5＝30通り（YとZの置き場所を決める）

できました☆

７▢▢▢▢▢

このとき、5×4＝20通りなんだから、６▢▢▢▢▢も４▢▢▢▢▢も同様に20通りになるね。

20×3＝60通り

場合の数＝場合分け、この問題だと10万の位が7の場合は、6の場合は、4の場合は、てことだね。あきらめずに根気をもって取り組もう。

よって、答えは60通りとなる。

にほんブログ村

中学校受験ランキング

場合の数１８。

 【 問題 】３～４年生向け

９９１、３００、５７５、８０８、のように2種類の数字からできている3けたの整数は何通りありますか。

【 解答 】

前回とまったく同じだね。慣れるまで根気よく手を動かそう。

では、まいります。

3けたの整数とある。百の位に0は使えないから、2種類の数字に0があるかないかで場合分けしてあげる。

【１】2種類の数字に0がある場合

2種類の数字の選び方は、（0、1）（0、2）（0、3）・・・（0、9）、の9通りある。

（0、1）のときを考えてみる。

百の位に0は使えないから、百の位は必ず1になる。

1▢▢

この▢には0か1が入るから

2×2＝4通り

なんだけど、111は使ってる数字が1種類になってしまうからダメ、引いてあげる。

4－1＝3通り

ちなみに、この3通りは

100、101、110

だね。

これくらいなら数えた方が断然速いね！

（0、1）のときが3通りなら、他の（0、2）（0、3）・・・（0、9）もそれぞれ3通りのはず。

3×9＝27通り

【２】2種類の数字に0がない場合

2種類の数字の選び方は、（1、2）（1、3）・・・、何通りだろうか。

0を除いた1～9の9個の数字から2個を選ぶんだから

9×8÷2＝36通り

2種類の数字の選び方は36通りだね。

（1、2）のときを考えてみる。

▢▢▢

この▢には1か2が入るから

2×2×2＝8通り

なんだけど、111と222は使ってる数字が1種類になってしまうからダメ、引いてあげる。

8－2＝6通り

ちなみに、この6通りは

112、121、122、211、212、221

だね。

これくらいなら数えた方が速いかもね！

（1、2）のときが6通りなら、他の場合もそれぞれ6通りのはず。

6×36＝216通り

【１】と【２】を足してあげたら答えだ。

27＋216＝243通り

どうだろ？ちょっとやれば身に付けられそうじゃない？

よって、答えは243通りとなる。

にほんブログ村

中学校受験ランキング

場合の数１７。

 【 問題 】５年生向け

１２１１、７０７０、５６６５、３８８８、４４４０、のように2種類の数字からできている4けたの整数は何通りありますか。

【 解答 】

場合の数は算数が得意な子にとっても厄介だと思う。なぜなら、整合性の確認、検証がしづらいからだ。丁寧に数え上げるという作業が大事なので、丁寧さを心掛けて欲しい。

では、いきましょう。

4けたの整数とある。千の位に0は使えないから、2種類の数字に0があるかないかで場合分けしてあげる。

【１】2種類の数字に0がある場合

2種類の数字の選び方は、（0、1）（0、2）（0、3）・・・（0、9）、の9通りある。

（0、1）のときを考えてみる。

千の位に0は使えないから、千の位は必ず1になる。

1▢▢▢

この▢には0か1が入るから

2×2×2＝8通り

なんだけど、1111は使ってる数字が1種類になってしまうからダメ、引いてあげる。

8－1＝7通り

（0、1）のときが7通りなら、他の（0、2）（0、3）・・・（0、9）もそれぞれ7通りのはず。

7×9＝63通り

【２】2種類の数字に0がない場合

2種類の数字の選び方は、（1、2）（1、3）・・・、何通りだろうか。

0を除いた1～9の9個の数字から2個を選ぶんだから

9×8÷2＝36通り

2種類の数字の選び方は36通りだね。

（1、2）のときを考えてみる。

▢▢▢▢

この▢には1か2が入るから

2×2×2×2＝16通り

なんだけど、1111と2222は使ってる数字が1種類になってしまうからダメ、引いてあげる。

16－2＝14通り

（1、2）のときが14通りなら、他の場合もそれぞれ14通りのはず。

14×36＝504通り

【１】と【２】を足してあげたら答えだ。

63＋504＝567通り

簡単なようで難しいような、難しいようで簡単なような、場合の数はそんな感じ。ある程度は自分で書き出して、目で見て、納得できるといいね。

よって、答えは567通りとなる。

にほんブログ村

中学校受験ランキング

場合の数１６。

 【 問題 】１～３年生向け

2、2、3、3、3、4、4、4、4

上の9個の数字を使って3けたの整数を作ります。何通りの整数が作れますか。

【 解答 】

寒くなってきたし体調管理にも気を配って気を引き締めて、合格に向けて1日1日を大事に、手応えを感じながら進んで欲しい。

では、まいります。

場合の数は数え上げられるなら泥臭く丁寧に書き出していけばいいと思うけど、明らかに計算で導いた方が楽な場合は、正しい解き方を覚えた方がいい。

この問題も解けるなら何でもいいと思う。ここでは解き方を2つ提示してみるね。

【１】

・1種類の数字を使う場合

444、333

⇒ 2通り

・2種類の数字を使う場合

44▢ ・・・ 442、443の2通り

4▢4 ・・・ 424、434の2通り

▢44 ・・・ 244、344の2通り

2×3＝6通り

この6通りは、3を2個使う場合でも、2を2個使う場合でも同じだから

⇒ 6×3＝18通り

・3種類の数字を使う場合（2、3、4を使う場合）

これはいいね

⇒ 3×2×1＝6通り

よって、2＋18＋6＝26通り、になる。

【２】

2だけ3枚に満たなくて2枚しかない。もし2がもう1枚あると

3×3×3＝27通り

の3けたの整数ができる。

だって、百の位にも2、3、4が、十の位にも2、3、4が、一の位にも2、3、4が、それぞれ使えるでしょ。だから3×3×3になる。

でも、2は3枚ではなくて2枚なんだから、27通りのうち222だけが作れない。

だから、27－1＝26通り、になる。

受験は、みんなができる問題は自分も〇にする！が一番大事。それにプラスして自分の得意分野や得意問題があるとなおいいね！

よって、答えは26通りとなる。

にほんブログ村

中学校受験ランキング

速さ１８。

 【 問題 】４年生向け

分速64mで進むと7分12秒かかる距離を、分速▢mで進むと2分24秒かかります。▢に入る数字はいくつですか。

【 解答 】

数字を計算せずに置いておく（あとから約分する）という作業は中学生以降になっても必要になってくるから、「計算せずに置いておくと楽な場合がある」くらいは頭の片隅に入れておこう。

では、いきましょう。

速さ×時間＝距離

これを徹底する。

秒速には秒を、分速には分を、時速には時間（h）を掛けるんだ。

分速64mとあるから、7分12秒と2分24秒を分に直しておこうか。

（ 小数でも分数でも、秒→分をパッと直せるように練習すること！ ）

7分12秒＝7.2分

2分24秒＝2.4分

怪しいのが見えてきたね。そう、7.2分の×1/3が2.4分だね。

かかる時間が×1/3なら、速さは×3すればいいね。

できました☆

64m/分 × 7.2分 ＝ ▢m/分 × 2.4分

⇒ ▢ ＝ 64 × 3 ＝ 192

そう、逆比だね。

距離が同じとき、かかる時間が7.2分：2.4分＝3：1であれば、速さの比は1：3になる、だから、64m/分×3＝192m/分だね。

当たり前の積み重ねが受験算数だよ。

よって、答えは192となる。

にほんブログ村

中学校受験ランキング

時計算２。

 【 問題 】１～３年生向け

2025年10月14日(火)0時00分～2025年10月15日(水)0時00分の間に、長針と短針は何回重なりますか。ただし、10月14日(火)0時00分と10月15日(水)0時00分の2回は除きます。

【 解答 】

アナログ時計を手元に用意して確認して欲しい。

では、まいります。

長針は短針よりたくさん動くね、だから、長針は短針を追い越していって、追い越すたびに1回重なるんだ。

0時に重なったあと、1時台、2時台、3時台、、、と、〇時台ごとに1回ずつ重なるんだけど、重ならない時間帯がある。そう、11時台と23時台だ。

11時台て重ならないでしょ？11時からスタートして、（長針は短針を30°×11＝330°追いかけるんだけど）長針が短針に追いついたとき、11時が終わって12時になってるね。時計の針を動かして確認するんだよ！

11時台と23時台だけは重ならない、他は4時台でも5時台でも6時台でも12時台でも16時台でも20時台でもすべての時間帯で1回ずつ重なってる。くどいけど、時計の針を動かして確認するんだよ！

できました☆

1時台～23時台まで、◯時台は23回ある、でも、そのうち11時台と23時台の2回は重ならないから引いてあげないといけない。

23－2＝21回

ちなみに、もし最初の14日0時00分を含めると書いてあれば22回、さらに15日0時00分まで含めると書いてあれば23回になるね。

よって、答えは21回となる。

にほんブログ村

中学校受験ランキング

面積６。

 【 問題 】４～５年生向け

図の三角形ABCはABとACの長さが等しい二等辺三角形です。ADとDBの長さが等しいとき、直角三角形CDEの面積を求めなさい。

（ 2025 東海中学 大問7 ）

【 解答 】

2025年東海受験組、お疲れさまでした。

もう日付も変わった、簡単だったとか難しかったとか、そんなの関係ないから。

やり切った感があるかどうかが大事。

悔いがないなら今のまま努力を継続すればいいし、もしも悔いが残るなら、中学生になってから心機一転、気持ちを改めて頑張ればいいんだよ。

手も足も出なかった子がいたら、もうね、そんなの大人のせいにしちゃいなよ！。正しい努力の仕方を教えてもらってなかったんだよ！

みんな一緒、やるぞ！！！と決めたときがスタート、いつからでも頑張れるから。

では、さくっと概観します。

今年の東海は文章題が少なかったね。速さの出題もなし。

大問2、4、7の面積はどうだろ。

大問2は、過去問をちゃんと教えてもらえた子は余裕だったかも。

大問4は、若干作業が細かいもののみんな見たことのある典型問題だったかな。

大問7は、単純問題ではあるものの合否分け（ないし加点）では。

例年みたいに抜きん出た問題がなかったから、算数得意な子は過去問よりは良い点数が出せたかもね。

大問7をさくっと簡単に解説しよう。

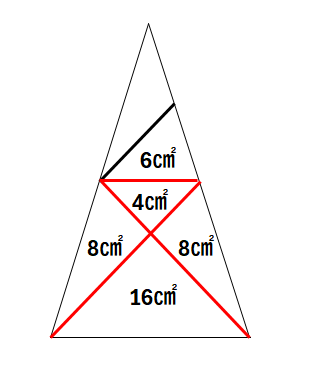
4＋8＝12

12× 3/2＝18㎠

等脚台形の対角線直交問題。

等脚台形 ⇒ 対角線直交 ⇒ △CDEにも相似

Ｄから右にBCとの平行線を引いて4cm、あとは45°に着目しながら、台形に対角線を引けば完成です。

Ｄから右にBCとの平行線を引いて4cm、これはみんなやったはず、そこからもう1本引けるかどうか。見たことある形に持ち込めるかどうか。

対角線が直交するが大事（小学校でも習う三角形の合同も大事）、この対角線直交の等脚台形は触れたことがある子も多いはず。

きれいにコンパクトにまとまった良問だと思います。

あまり難しすぎてもね、対策が大変になるし。これくらいで十分差がつくと思います。このレベルが定着した方が東海にとっても受験生にとってもプラスでは。

多くの子はまだ滝が残ってるね、最後の力を振り絞って頑張って！！！

にほんブログ村

中学校受験ランキング